机器学习-白板推导 5 降维

1. 降维 Dimension Reduction

机器学习中，最关心的是泛化误差，降低泛化误差是非常关键的。泛化误差和过拟合等关系图如下

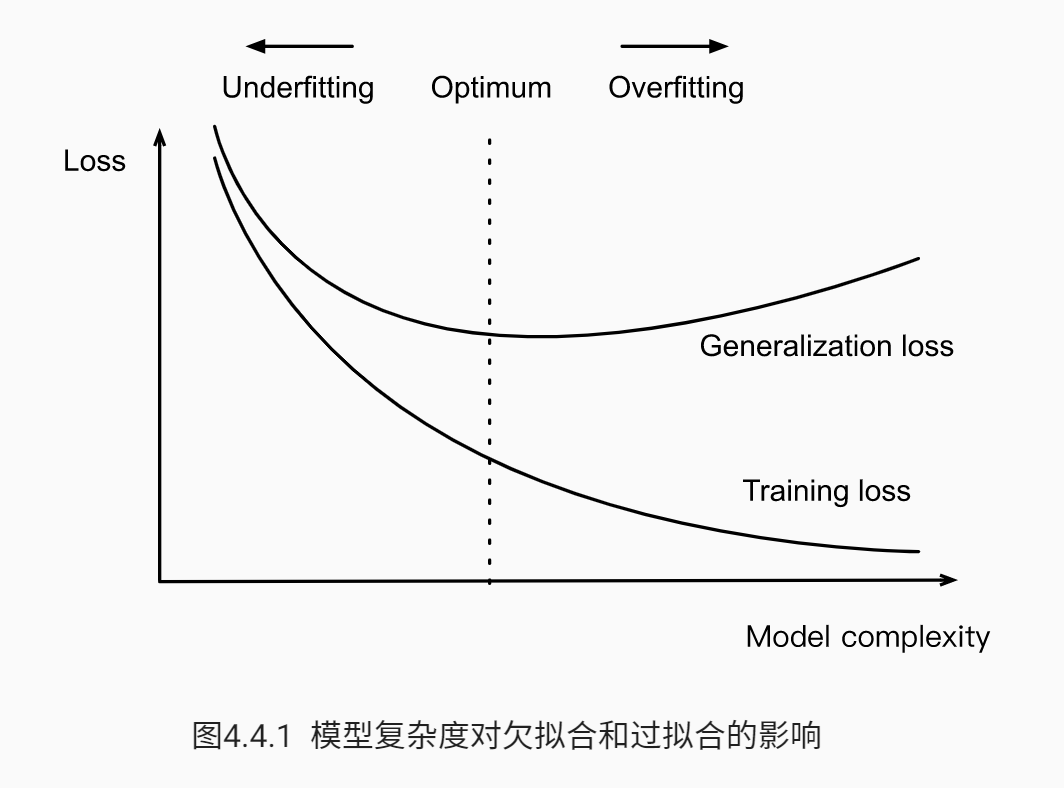
解决过拟合的方法有：

增加数据量
正则化，如Lasso和Ridge本质都是降维，Lasso会让部分 $w$ 趋于0，来消除一些特征。
降维

维度灾难：

高纬度有更大的特征空间，需要更多数据才可以拟合模型。若特征是二值的，则每增加一个特征，数据列都在以2的指数级增长，更何况很多特征不是二值的
几何角度：
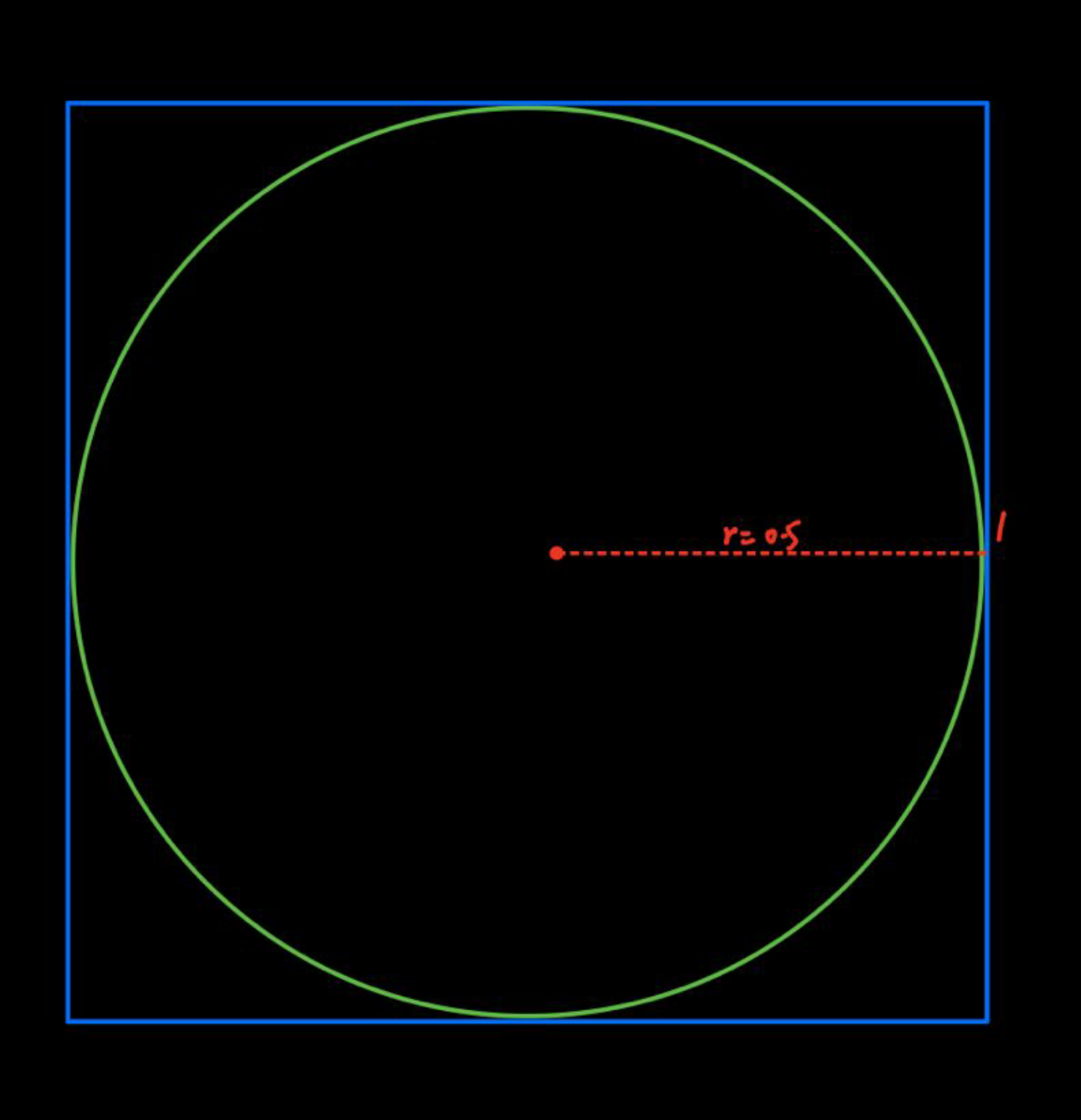
- 如下图所示，假定正方形边长为1，则其内切圆半径为0.5，正方形面积为1，圆面积为 $\pi(0.5)^2$ 。拓展到3维时，正方形体积为1，内切球体积为 $\frac{4}{3}\pi(0.5)^3$ 。

如下图所示，假设外圆半径为 $r=1$ ，则内圆半径为 $r- \epsilon = 1- \epsilon$ 。在高维情况下，外圆体积为 $V_外 = k1^D = k$ , 中间圆环体积为 $V_环= k - k(1-\epsilon)^D$ 。

那么有：
$\lim_{D \to 0} \frac{V_环}{V_外} = \lim_{D \to 0} \frac{k - k(1-\epsilon)^D}{k} = \lim_{D \to 0}1-(1-\epsilon)^D = 1$

从两个例子可以看出，高维情况下，数据占据着空间表明，内部趋于0，数据分布稀疏。

常用的降维方法：

直接降维：特征选择，将不重要的特征扔掉
线性降维：PCA， MDS(multidimensional scaling)
非线性降维：流形（将数据嵌入到高维空间），局部线性嵌入

2. 样本均值和方差的矩阵表示

后续PCA和SVD都是在矩阵上操作，所以先将均值和方差矩阵表示。

假设数据集为：

$\begin{equation} X=(x_1, x_2, \cdots, x_N)^T= \begin{pmatrix} x_1^T \\ x_2^T \\ \vdots\\ x_N^T \\ \end{pmatrix} = \begin{pmatrix} x_{11} & x_{12} & \dots & x_{1p}\\ x_{21} & x_{32} & \dots & x_{2p}\\ \vdots & \vdots & \ddots & \vdots\\ x_{N1} & x_{N2} & \dots & x_{Np}\\ \end{pmatrix}_{N\times P} \end{equation}$

其中 $x_i \in \mathbb{R}^p, \ i=1,2, \cdots, N$ 。

其样本均值为：

$\bar X_{p \times 1} = \frac{1}{N} \sum_{i=1}^N x_i \tag{1}$

样本方差为：

$S_{p \times p} = \frac{1}{N} \sum_{i=1}^N (x_i- \bar X)(x_i- \bar X)^T \tag{2}$

对式1， 2简化表示：

1. 均值

$\bar X = \frac{1}{N}\sum_{i=1}^N x_i=\frac{1}{N}(x_1 \quad x_2 \quad \cdots \quad x_N) \begin{pmatrix} 1\\ 1 \\ \vdots\\ 1 \\ \end{pmatrix} = \frac{1}{N}X^T1_{N \times 1}= \frac{1}{N}X^T1_{N }\tag{3}$

其中， $1_{N}=1_{N \times 1} = \begin{pmatrix} 1\\ 1 \\ \vdots\\ 1 \\ \end{pmatrix}$ 。

2. 方差

$\begin{align} S_{p \times p} &=\frac{1}{N} \sum_{i=1}^N (x_i- \bar X)(x_i- \bar X)^T\\ &=\frac{1}{N}(x_1 - \bar X\quad x_2- \bar X \quad \cdots \quad x_N- \bar X) \begin{pmatrix} (x_1 - \bar X)^T\\ (x_2 - \bar X)^T\\ \vdots\\ (x_N - \bar X)^T\\ \end{pmatrix}\\ &=\frac{1}{N}(X^T(I_N- \frac{1}{N}1_{N }1_{N }^T))(X^T(I_N- \frac{1}{N}1_{N }1_{N }^T))^T\\ &= \frac{1}{N}X^T(I_N- \frac{1}{N}1_{N }1_{N }^T)(I_N- \frac{1}{N}1_{N }1_{N }^T)^TX\\ &= \frac{1}{N}X^THH^TX\\ \end{align} \tag{4}$

其中，

$\begin{align} &(x_1 \quad x_2 \quad \cdots \quad x_N) - (\bar X\quad \bar X \quad \cdots \quad \bar X)\\ &= (x_1 \quad x_2 \quad \cdots \quad x_N) - \bar X(1 \quad 1 \quad \cdots \quad 1)\\ &= X^T-\bar X1_{1 \times N}\\ &= X^T-\frac{1}{N}X^T1_{N }1_{N }^T\\ \end{align}$

而 $H = I_N- \frac{1}{N}1_{N }1_{N }^T$ ，叫做 centering matrxi。并且有 $H^T=H, H^2=H$ ，那么式4进一步化简得：

$S =\frac{1}{N}X^THX \tag{5}$

3. PCA

PCA基本思想是将所有数据投影到一个子空间取，从而达到降维的目的。这个子空间要满足：

最大可分性：样本点在这个超平面上的投影尽可能分开，所有数据在子空间中更为分散。
最近重构性：样本点到这个平面的距离足够近，那么损失的信息最少，即在补空间上的分量小。

关键思想:

一个中心：将原始特征空间重构，将线性相关的特征转化为线性无关的特征。
两个基本点：最大投影方差和最小重构距离.

如下图所示，将原始数据分别投影到 $\mathbf{u}_1, \mathbf{u}_2$ ,在 $\mathbf{u}_1$ 方向更为分散，因而选择往这个方向投影。

PCA降维步骤：

数据去中心化 ，就是减去均值，一定得去中心化。
投影到一个新的方向上，这个新的方向就是重构的特征空间的坐标轴，并且要满足投影后得到的数据的方差最大，即最大投影方差，这样同时也保证了数据重构的距离最小。

4. 最大投影方差理解PCA

假设投影方向为 $\mathbf{u}$ , 并且将其模设为1， $u^Tu =1$ ,那么原数据去中心化后的数据在 $\mathbf{u}$ 方向上的投影为 $(x_i - \bar x)^Tu$ ，又因为去中心化后均值为0，所以投影方差为 $((x_i - \bar x)^Tu)^2$ 。

那么目标函数为：

$\begin{align} J &= \frac{1}{N} \sum_{i=1}^N((x_i - \bar x)^Tu)^2 \quad s.t. \ u^Tu=1 \\ &= \frac{1}{N} \sum_{i=1}^Nu^T(x_i -\bar x)(x_i - \bar x)^Tu \\ &= u^T(\frac{1}{N} \sum_{i=1}^N(x_i -\bar x)(x_i - \bar x)^T)u \\ &= u^T Su \end{align} \tag{6}$

其中 $S = \frac{1}{N} \sum_{i=1}^N(x_i -\bar x)(x_i - \bar x)^T$ 是协方差矩阵。

使用拉格朗日乘子法：

$L(u, \lambda) = u^TSu + \lambda(1-u^Tu) \tag{7}$

对 $u$ 求导得：

$\frac{\partial L}{\partial u} = 2Su - 2\lambda u=0 \Longrightarrow Su = \lambda u\tag{8}$

其中 $S$ 是协方差矩阵， $\lambda$ 是特征值， $u$ 是特征向量。那么只要将协方差矩阵S进行特征值分解，将求得的特征值排序，取需要的前p个，在计算出对应的特征向量，就是PCA的解。

5. 最小重构距离理解PCA

去中心化后数据为 $x_i ^\prime=x_i - \bar x$ , 假设我们将其投影到对应空间后，取前p个特征有：

${\hat x^\prime}_i = \sum_{k=1}^p ({x^\prime_i}^Tu_k)u_k \tag{9}$

假定 $u_i$ 已经按照特征值 $\lambda_i$ 从大到小排列。

那么目标函数为(去中心数据点到投影点的距离最小),本质上源空间有p个特征，如果降维后选取了q个特征，降维的数据也就是舍弃掉第q+1到第p这几个方向上的信息。

$\begin{align} J &=\frac{1}{N} \sum_{i=1}^N \lVert x_i ^\prime-{\hat x^\prime}_i\rVert^2 \quad \ s.t. \ u_k^Tu_k=1 \\ &= \frac{1}{N} \sum_{i=1}^N \sum_{k=q+1}^p ((x_i-\bar x)^Tu_k)^2 \\ &= \sum_{k=q+1}^p\frac{1}{N} \sum_{i=1}^N ((x_i-\bar x)^Tu_k)^2 \\ &=\sum_{k=q+1}^p u^TSu_k \end{align} \tag{10}$

式10跟式7一样有：

$Su_k = \lambda_ku_k \tag{11}$

这里 $u_k$ 为协方差矩阵的前k个特征向量。

6. SVD角度看PCA

SVD介绍，如果我们先对数据 $X$ 去中心化，左乘中心矩阵H(在上面第3部分)，然后进行SVD分解，因此有：

$HX = U\Sigma V^T \tag{12}$

其中，

$U$ 是 $N \times N$ 的矩阵，并且 $U^TU=UU^T=I$ 。
$V$ 是 $P \times P$ 的矩阵，并且 $V^TV=VV^T=I$ 。
$\Sigma$ 为 $N \times P$ 的矩阵，且是对角阵。

式5中 $S =\frac{1}{N}X^THX$ , 因此：

$\begin{align} S &=\frac{1}{N}X^THX \qquad \text{由于}\frac{1}{N}\text{是常数简化计算忽略}\\ &= X^TH^THX\\ &= (HX)^THX \\ &= (U\Sigma V^T)^T U\Sigma V^T\\ &= V\Sigma^T U^T U\Sigma V^T\\ &= V\Sigma^T \Sigma V^T\\ &= V\Sigma^2 V^T \end{align} \tag{13}$

那么 $V\Sigma^2 V^T$ 是 $S$ 的特征值分解， $\Sigma^2$ 是特征值矩阵。

若我们构造矩阵 $T_{N \times N}$ 如下：

$T_{N \times N} = HXX^TH^T =U\Sigma V^T V\Sigma^T U^T=U\Sigma \Sigma^T U^T \tag{14}$

将 $S$ 进行特征分解后得到主成分，将 $X$ 投影到主成分的方向后，其坐标为 $HX \cdot V = U\Sigma V^TV = U\Sigma$
而直接对 $T$ 进行特征分解，坐标矩阵 $U \Sigma$ ，这种方法叫主坐标分析 PCoA ——Principle Coordinate Analysis。

原因： $TU\Sigma = U\Sigma \Sigma^T U^T U \Sigma = U \Sigma \Sigma^T \Sigma$ , （就是将式14代入），那么有 $T U \Sigma = U\Sigma (\Sigma^T\Sigma)$ ,这里 $\Sigma^T\Sigma$ 是特征值， $U\Sigma$ 就是坐标。